Tanh(x) - 하이퍼볼릭 탄젠트의 고차미분
y = tanh(x) = (exp(x)+ exp(-x)) / (exp(x) + exp(-x)) 함수를 예시로 살펴보자.

이 함수의 미분형태를 살펴보면 ,1-y^2 으로 표현이 가능하다는 것을 알 수 있다.
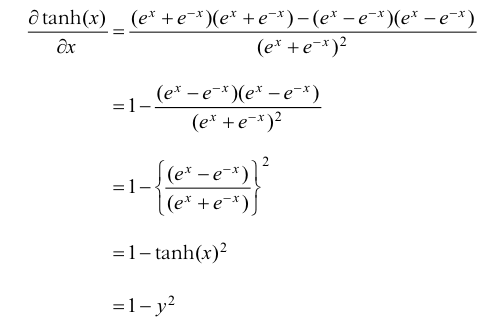
이 함수를 간단하게 구현해보면, 이와 같은 코드가 된다.
class Tanh(Function):
def forward(self,x) :
y = np.tanh(x)
return y
def backward(self,gy) :
y = self.outputs[0]()
gx = gy * (1- y*y)
return gx
def tanh(x):
return Tanh()(x)이때, 1차 미분 계산 그래프를 그려보면,
import numpy as np
from dezero import Variable
from dezero.utils import plot_dot_graph
import dezero.functions as F
x = Variable(np.array(1.0))
y = F.tanh(x)
x.name = 'x'
y.name = 'y'
y.backward(create_graph =True)
iters = 0 # 1차미분일때의 값
for i in range(iters) :
gx = x.grad
x.cleargrad() # Variable x의 gradient값을 None 으로 초기화 해준후,
gx.backward(create_graph= True) # 역전파 해준다.
gx = x.grad # 계산 그래프를 그리기 위한 식을 넘겨준다.
gx.name = 'gx' + str(iters+1)
plot_dot_graph(gx,verbose = False, to_file = 'tanh.png')해당 그래프의 결과를 Dot 파일에서 png 파일로 변환 후 나타내면
Tanh(x)의 1차미분 그래프를 그릴 수있다.
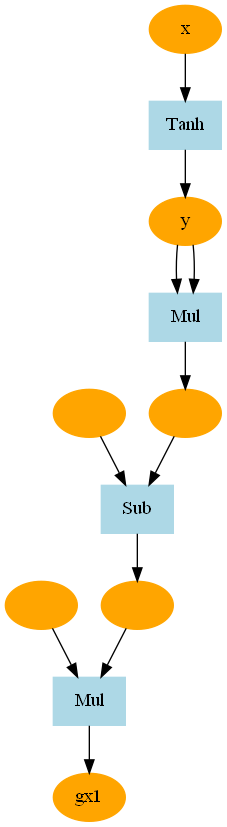
위 식을 이용해서 5차 미분계수를 나타내보면 , 이와 같이 나타낼 수 있다.

'# AI 이론 > DeepLearning' 카테고리의 다른 글
| 배치 정규화 (0) | 2022.04.20 |
|---|---|
| 케라스를 이용한 인공 신경망 만들기(하이퍼파라미터 튜닝) (0) | 2022.04.19 |
| 케라스를 이용한 이미지 분류기 만들기 (0) | 2022.04.18 |
| 밑바닥부터 시작하는 딥러닝3 내용정리 (0) | 2022.03.21 |
| 합성곱 신경망(CNN) (2) | 2022.03.03 |