
Class(Variable, Function)
전체 코드를 가져오기에는 길기 때문에 일부 부분씩을 캡쳐하여 정리함
●Variable
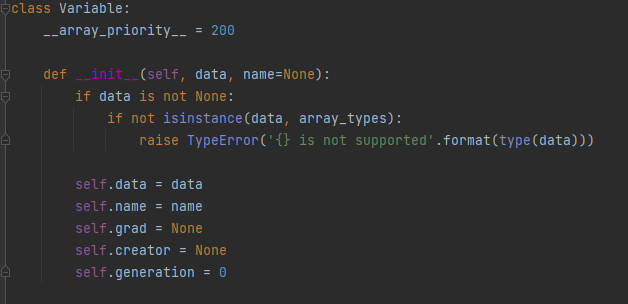
- Variable 클래스 생성(params : 데이터,변수명,기울기,함수,현재의 세대)
- data : isinstance 메서드를 통해서 cupy,ndarray 인스턴스만을 받음
- name : 이후 Layer 계층에서의 params.__dict__[name]의 형태로 호출
- grad : gradient 로, Backpropagation 시 기울기를 저장
- creator : input Data ----- Function ------ output Data 에서 , output Data는 Function에서 만들어진 것처럼, 자기자신의 생성자를 저장(해당 함수를 저장함)
- 데코레이터(@)를 이용하여, 클래스 인스턴스의 함수 호출을 편리하게 만들수 있음.
- __repr__ : print(클래스 인스턴스) 실행시, 해당 코드가 실행
- __len__ : data의 길이를 호출하도록 Wrapper

- backward() : backpropagation 함수로, params 는 2개를 가지고있다.
- retain_grad : 역전파시, 미분값들을 저장할것인가? -> 메모리의 절약을 기대할 수 있음
- funcs : 현재 함수의 값을 리스트로 저장함
- 내부적으로 add_func(f) 함수가 저장되어있는데, 순전파의 역순서대로 함수를 실행하도록 값을 저장
gys = [output().grad for output in f.outputs] 의 방식에서 ,역전파는 결과에서 부터 시작 방향으로 출발하므로
outputs의 gradient 값들을 저장
(outputs들은 순전파를 시행할때 이미 저장되어있는 값들)
- with using_config : 해당 with 문내에서만 역전파 코드를 시행할것인가 하지 않을것인가를 저장
역전파의 경우 다음과 같은방향으로 흘러가기 때문에, gy 와 Function 을통해서 gx 값을 구해나가는 과정

- zip(f.inputs,gxs) 값을 통해서 , x의 gradient 값들을 갱신해 나간다.

●Function
- __call__ : Function 클래스의 인스턴스 객체를 호출시에 실행되는 함수로,
인자로, *inputs 을 받는다. (* 는 가변인자 라는의미) - xs : Function의 inputs값들을 담을 리스트
- ys : forward를 수행하면, 순전파 시 , Function 함수의 결과값들을 반환한다. 그값들을 Outputs이라는 리스트에 Variable 인스턴스로 저장 ( Variable 로 저장을 해야 Gradient를 담을 수 있음)
- Config 클래스는 역전파를 수행할지 말지 정하는 클래스로 정함
- output.set_creator(self) 를 통해, 각 Variable의 Creator(Function)을 저장
- forward,backward 의 경우 상속을 통해서 수행

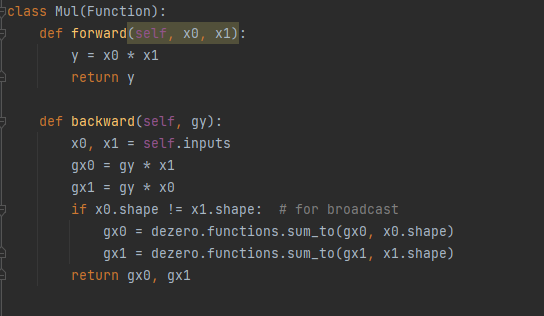
함수의 종류가 다양하므로 대표적으로, Divide 와 Multiply 만 살펴보자
- 순전파 시에는 두개의 값을 곱한뒤 반환한다.
- 역전파 시 y = x0 * x1 에서 두개의 변수가 다르므로 편미분을 통해서 구해준다.
gx0 ,gx1을 다음과 같이 구할 수 있다.
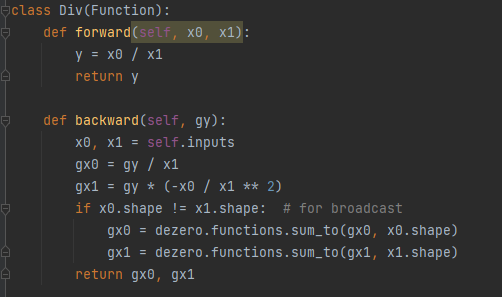
- 순전파 시에는 두개의 값을 나누어서 반환
- 역전파 시에는 x0/x1의 경우 x0에 대한 편미분은 분자만 미분하면 되지만, x1에 대한 편미분은 수학공식에 따라서 수행
이후 인스턴스가 함수를 호출할때, 편리성을 위해 다음과 같이 메서드를 생성
- 연산을 수행할때마다 함수를 호출할 경우, 다항식에서 복잡하기 때문에 연산자 오버로드를 통해서 편리하게 만들 수 있다.
- setup_variable() 메서드에 Variable 연산자 오버로딩


Layer(Linear,Conv2d),MAX Pooling
- Layer는 계층을 표현하는 클래스로 , Layer 내 구성은 간단하게 다음과 같이 나타낼 수 있다.

- Layer 클래스의 params으로는 _params 이라는 집합형set()을 이용한다. (중첩방지)
- _params 내에는 Parameter 혹은 Layer만을 저장한다.
- __call__ 함수를 통해서 , input , output data를 저장한다.
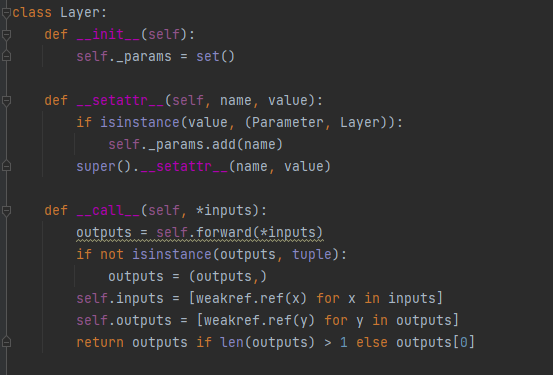
- forward 메서드는 Linear,Conv2d,RNN 등의 함수에서 상속하여 사용할 예정
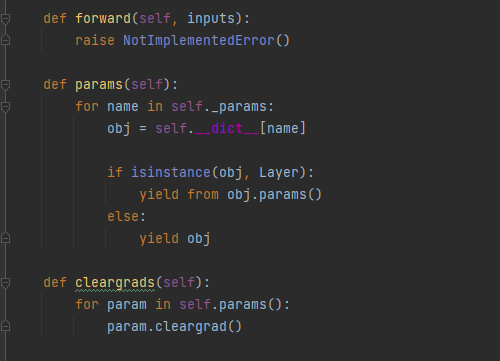
- params() 메세드를 통해서 해당 Layer내에 있는 Layer,Parameter를 yield를 통해서 순차적으로 return 한다.
- cleargards() 를 통해서 해당 Layer의 params의 기울기를 초기화
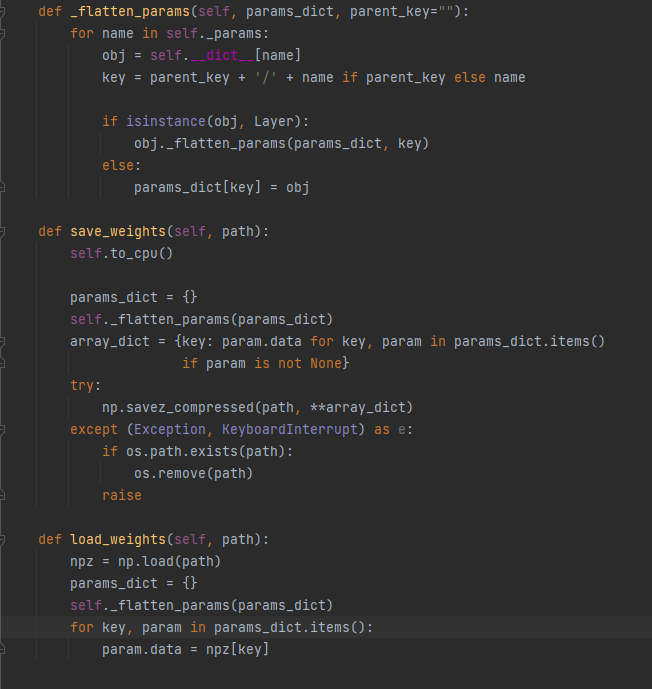
- 위의 그림처럼,layer 라는 클래스 내에 Layer L1 과 Parameter p2,p3 가 저장되어있고, Layer L1에 p1 이라는 Parameter 인스턴스가 저장되어 있을때, 저장되어 있는 객체를 꺼내기 위한 함수가 _flatten_params 이다.
해당 반환값 : params_dict = {'p2' : Parameter' , 'p3' : Parameter, 'l1/p1' : Parameter} 로 출력 - save_weights , load_weights 메서드의 경우는 외부파일에 값들을 저장하고 꺼내올 때 사용함
●Linear(Class,Function)
- 선형회귀를 구현하는 계층
- out_size : 출력데이터의 크기
- in_size : 입력데이터의 크기
- forward 에서 F.linear(x,W,b)로 인자를 넘겨서 선형회귀 함수를 시행
▶Class

- 순전파 시, Y = X * W +b를 통해 y값 output을 리턴
- 역전파 시, 다음과 같이 gx = gy * W.T , gW = x.T * gy 로 구할 수 있다.

▶Function

●Convolution 2d(Class,Function)
- 합성곱 신경망은 이전의 글에서 정리했으므로, 설명은 생략
- out_channels : 출력데이터의 크기
- kernel_size : 커널,필터의 크기(pair 함수를 통해 정방행렬일 경우 정수 하나만 입력가능)
- stride : 스트라이드(몇칸씩 띄엄띄엄 할건지)
- pad : 기존 데이터의 padding을 넣어 데이터의 크기가 줄어드는것을 방지
- in_channels : 입력데이터의 크기
▶Class

▶Function
- 입력데이터, 커널, 스트라이드,패드의 데이터를 받은뒤 출력데이터의 크기를 계산
- im2col 함수를 통해서 4차원의 데이터를 2차원의 데이터로 flattening (to_matrix = True 를통해서 행렬곱이 가능한 형태로 반환)
- Weight는 4차원 데이터이므로 2차원의 데이터와 행렬곱을 하기위해 reshape과 transpose를 통해서 변환 및 전치
- linear 함수를 통해서 계산 후 transpose를 통해서 (N,OC,OH,OW)형태로 변환

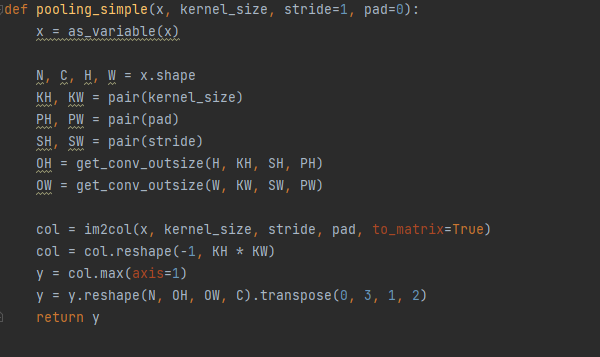
●MAX Pooling
- 위와 같이 Input Data ,Stride ,pad 를 통해서 OH,OW를 계산
- im2col 를 통해서 2차원데이터로 flattening 후 col 를 reshape(-1,KH*KW)형태로 변환
- 각 행마다의 최대값을 저장 후 reshape,transpose를 통해서 4차원데이터로 재변환
Model(MLP)
●MLP (Multi Layer Perceptron 다층 퍼셉트론)
- tuple 형태의 인자와 활성화 함수를 인자로 받는다.
- fc_output_sizes 는 Tuple 이나 리스트 형태로 지정하기 때문에, 2개의 Layer일경우 (10,1)을 건네면 2개의 Linear 계층을 만들고 첫번째 출력크기은 10 , 두번째 계층의 출력 크기는 1로 구성
- forward 함수를통해서 각 layer마다 선형회귀 후 활성화 함수를 수행 해준다.(ReLU,Sigmoid 등등 )

Optimizers(SGD,MomentumSGD...)
- 매개변수 갱신을 위한 기반 클래스
- target,hooks 두개의 인스턴스 변수를 초기화
- setup 메서드는 매개변수를 갖는 클래스(Model or Layer)를 인스턴스 변수인 target으로 설정
- update 메서드는 모든 매개변수를 갱신 (grad = None 인것은 건너뜀 )
- update_one 메서드는 Optimizer의 자식클래스에서 재정의
- add_hook 함수는 전처리를 수행하는 함수를 추가

▶SGD
- 확률적 경사하강법으로, x = x - learning_rate * x.grad 의 식을 이용

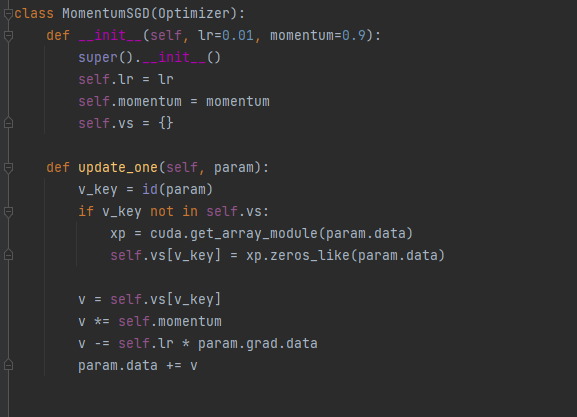
▶Momentum
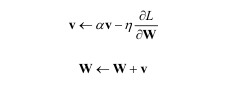
- W : 갱신할 가중치 매개변수
- gL/gW : W에 대한 손실함수 L의 기울기
- v : 속도
- av : 물체가 아무런 힘을 받지않을 때 서서히 감속시키는 역할(a = 0.9등으로 설정)
- v_key = id(param)에서 각 param을 고유하게 식별하기 위해 id 메서드를 사용
- vs는 속도를 담는 딕셔너리
- 마지막 4줄은 위의 공식을 계산
'# AI 이론 > DeepLearning' 카테고리의 다른 글
| 배치 정규화 (0) | 2022.04.20 |
|---|---|
| 케라스를 이용한 인공 신경망 만들기(하이퍼파라미터 튜닝) (0) | 2022.04.19 |
| 케라스를 이용한 이미지 분류기 만들기 (0) | 2022.04.18 |
| 밑바닥부터 딥러닝3 - 고차 미분 (0) | 2022.03.14 |
| 합성곱 신경망(CNN) (2) | 2022.03.03 |