- 그래디언트 소실과 폭주
- 배치 정규화
그레이디언트 소실과 폭주문제
역전파 알고리즘은 출력층에서 입력층으로 오차 그레이디언틀르 전파하면서 진행합니다.
이때 알고리즘이 신경망의 모든 파라미터에 대한 오차 함수의 그레이디언트를 계산하면 경사 하강법 단계에서 이 그레이디언트를 사용하여 각 파라미터를 수정하게 됩니다.
그런데 알고리즘이 하위층으로 진행될수록 그레이디언트가 점점 작아지는 경우가 많아지는데,
경사 하강법이 하위층의 연결 가중치를 변경되지 않은 채로 둔다면 안타깝게도 훈련이 좋은 솔루션으로 수렴되지 않을 것 입니다. 이 문제를 그레이디언트 소실(vanishing gradient) 라고합니다.
위와 반대로 그레이디언트가 점점 커져서 여러 층이 비정상적으로 큰 가중치로 갱신되면 알고리즘은 발산합니다.
이 문제를 그레이디언트 폭주(exploding gradient) 라고합니다.
그렇다면 그레이디언트를 불안정하게 만드는 요인이 무엇일까?
로지스틱 시그모이드 활성화 함수와 가중치 초기화 방법에 영향이 컸습니다.
이 활성화 함수와 초기화 방식을 사용했을 때 각 층에서 출력의 분산이 입력의 분산보다 크다는 것이 밝혀졌습니다.
글로럿과 He 초기화
그레이디언트를 전파할때는 양방향 신호가 적절하게 흘러야 합니다.
신호가 적절하게 흐르기 위해서는 다음과 같습니다.
- 각 층의 출력에 대한 분산이 입력에 대한 분산과 같아야 한다
- 역방향에서 층을 통과하기 전과 후의 그레이디언트 분산이 동일해야 합니다
- 입력과 출력 연결 개수(fan-in , fan-out)가 같지 않으면 이 두가지를 보장할 수 없습니다
세이비어 초기화(Xavier initialization)
fan_avg = (fan_in + fan_out ) / 2
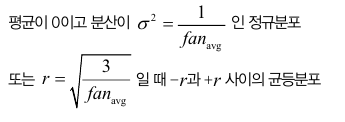
이 식에서 fan_avg를 fan_in으로 바꾸면 르쿤 초기화 라고부릅니다.
| 초기화 전략 | 활성화 함수 | 정규분포(분산) |
| 글로럿 | 활성화 함수없음,tanh(x),logistic,softmax | 1/fan_avg |
| He | ReLU 함수와 그 변종들 | 2/fan_in |
| 르쿤(lecun) | SELU | 1/fan_in |
ReLU 와 SELU방식의 사용법을 보면 다음과 같습니다.
# ReLU 방식과 He 초기화
keras.layers.Dense(300,activation="relu",kernel_initalizer="he_normal")
# SeLU 방식과 Lecun 초기화
keras.layers.Dense(300,activation="selu",kernel_initalizer="lecun_normal")fan_in 대신 fan_avg 기반의 균등분포 He 초기화를 사용하고 싶다면 다음과 같이 사용할 수 있습니다.
he_avg_init = kears.initializers.VarianceScaling(scale=2., mode='fan_avg',distribution="uniform")
keras.layers.Dense(10, activation="sigmoid",kernel_initalizer=he_avg_init)
수렴하지 않는 활성화 함수
이전까지는시그모이드 활성화 함수가 최선의 선택일것이라고 생각했습니다. 하지만 다른 활성화 함수가 심층 신경망에서 훨씬 더 잘 작동한다는 사실이 밝혀졌습니다.
특히 ReLU 함수는 특정 양숫값에 수렴하지 않는다 와 계산이 빠르다라는 장점이 있습니다.
하지만 이 ReLU 함수는 완벽하지 않는데 죽은 ReLU 문제가 존재합니다.
훈련하는동안 일부 뉴런이 0이외의 값을 출력하지 않는다는 의미에서 죽었다고 말합니다.
가중치 합이 음수이면 ReLu 함수의 그레이디언트가 0이 되므로 경사 하강법이 더는 작용하지 않기때문에 이애대한 해결책으로 ReLU 변종을 사용합니다.
LeakyReLU
하이퍼 파라미터 alpha 값이 새는(leaky) 정도를 결정하는데, 새는 정도란 z <0일때 이 함수의 기울기이며, 일반적으로 0.01로 설정합니다. 이 작은 기울기가 LeakyReLU 함수를 절대 죽지않게 만듭니다.


ELU
이 함수의 주요 단점은(지수 함수를 사용하므로) ReLU나 그 변종들보다 계산이 느리다는 것입니다.
훈련하는 동안에는 수렴 속도가 빨라서 느린 계산이 상쇄되지만 테스트 시에 ELU를 사용한 네트워크가 ReLU를 사용한 네트워크보다 느립니다


SELU
스케일된 ELU 활성화 함수의 변종으로, 완전 연결층(Full Connected Layer)만 쌓아서 신경망을 만들고 모든 은닉층이 SELU 활성화 함수를 사용한다면 네트워크가 자기 정규화가 된닷는것을 보였습니다.
자기정규화가 되기 위한 몇가지 조건을 살펴보면
- 입력 특성이 반드시 표준화(mean = 0 , std = 1) 이어야 합니다.
- 모든 은닉층의 가중치는 lecun_normalization으로 초기화 되어있어야합니다.
- 네트워크는 일렬로 쌓은 층으로 구성되어야 합니다. 순환신경망이나 스킵연결과 같은 순차적이지 않은 구조에 SELU를 사용하게 되면 자기 정규화가 되는것을 보장하지 않습니다.

100개의 은닉층과 SELU 활성화 함수를 사용한 패션 MNIST 신경망 만들기
모델을 생성 → 활성화 함수는 SELU, 초기화는 lecun 방식 / 출력층은 10개의 클래스를 받으므로 10, softmax
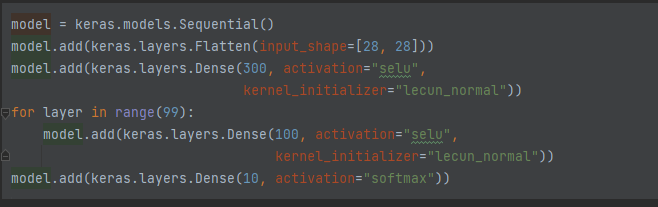
model을 compile() 메서드를 통해 loss, optimizer,metrics 설정

훈련을 시작하기전, 입력데이터의 평균과 표준편차를 0과 1로 바꾸어야 합니다
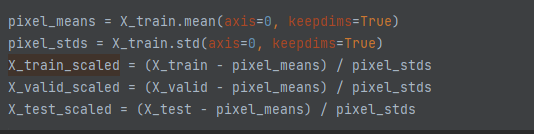

각 에포크당 결과 입니다.
Epoch 1/5
1719/1719 [==============================] - 27s 14ms/step - loss: 1.2359 - accuracy: 0.5200 - val_loss: 0.8552 - val_accuracy: 0.6756
Epoch 2/5
1719/1719 [==============================] - 23s 13ms/step - loss: 0.7186 - accuracy: 0.7408 - val_loss: 0.6080 - val_accuracy: 0.7830
Epoch 3/5
1719/1719 [==============================] - 24s 14ms/step - loss: 0.6907 - accuracy: 0.7527 - val_loss: 0.6446 - val_accuracy: 0.7532
Epoch 4/5
1719/1719 [==============================] - 23s 13ms/step - loss: 0.6234 - accuracy: 0.7805 - val_loss: 0.6986 - val_accuracy: 0.7346
Epoch 5/5
1719/1719 [==============================] - 24s 14ms/step - loss: 0.6030 - accuracy: 0.7859 - val_loss: 0.7600 - val_accuracy: 0.7390
배치 정규화(Batch Normalization)
앞서 ELU와 함께 He 초기화를 사용하면 훈련 초기 단계에서 그레이디언트 소실이나 폭주문제를 크게 감소시킬 수 있지만, 훈련하는 동안 다시 발생하지 않으리란 보장은 없습니다.
이를 해결하기위해 배치 정규화라는 기법이 있는데 살펴보겠습니다.
배치정규화는 평균과 분산을 조정하는 과정이 별도의 과정으로 떼어진 것이 아니라, 신경망 안에 포함되어 학습 시 평균과 분산을 조정하는 과정으로, 각 레이어마다 정규화 하는 레이어를 두어, 변형된 분포가 나오지 않도록 조절하는것 입니다.

- 우선 Input으로 사용된 미니배치의 평균과 분산을 계산
- 은닉층의 활성화값/출력값에 대해서 평균과 분산을 0,1되도록 정규화
- 배치 정규화 단계마다 확대와 이동변환을 수행
Training 시 mini-batch 평균과 분산으로 정규화를 실시하고, Test 할때는 계산해놓은 이동 평균으로 정규화를 한다. 정규화후에는 scale factor 와 shift factor를 이용하여 새로운 값을 만들고 이 값을 내놓는다.
Scale factor, Shift factor의 경우 다른 레이어에서 가중치 학습 하듯이 역전파에서 학습하면 된다
케라스를 이용한 간단한 배치정규화 모델 만들기
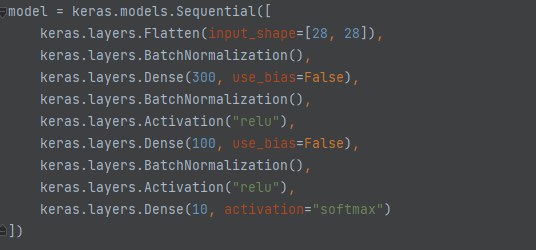
은닉층의 활성화 함수 전이나 후에 BatchNormalization 층을 추가 해주면 구현할 수 있습니다.
배치 정규화 층은 입력마다 4개의 파라미터가 존재하는데,
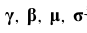
첫번째,두번째 파라미터는 역전파를 통해 학습되는 파라미터로 Trainable 파라미터로 분류하고
세번째 네번째 파라미터는 역전파로 학습되지 않기 때문에 Non-trainable 파라미터로 분류합니다(이동평균)
이번엔 그레이디언트 폭주/소실, 다양한 활성화함수, 배치정규화에 대해서 정리해보았습니다.
'# AI 이론 > DeepLearning' 카테고리의 다른 글
| TensorFlow Protocol Buffer (0) | 2022.04.26 |
|---|---|
| 규제를 사용해 과대적합 피하기 (0) | 2022.04.20 |
| 케라스를 이용한 인공 신경망 만들기(하이퍼파라미터 튜닝) (0) | 2022.04.19 |
| 케라스를 이용한 이미지 분류기 만들기 (0) | 2022.04.18 |
| 밑바닥부터 시작하는 딥러닝3 내용정리 (0) | 2022.03.21 |