- 선형회귀 및 경사하강법(배치 경사하강법, 미니배치 경사하강법, 경사하강법)
- 다항회귀
- 규제가 있는 선형 모델
선형회귀
입력 특성의 가중치 합과 편향 이라는 상수를 더해 예측을 만든다.

- y는 예측값
- n은 특성의 수
- xi 는 i 번째 특성값
- 세타는 j번째 모델 파라미터

와 같이 표현이 가능하다.
▷ 선형 회귀 모델의 MSE 비용 함수
𝜽 값의 MSE(𝜽) 는 다음과 같이 표현할 수 있다.
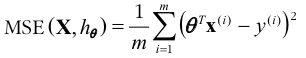
이때 비용함수의 값을 최소화 하는 𝜽 를 얻을 수 있는 공식이 있는데, 다음과 같다.
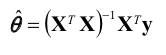
경사 하강법
경사하강법 이란?
- 여러 종류의 문제에서 최적의 해법을 찾을 수 있는 일반적인 최적화 알고리즘
- 비용 함수를 최소화 하기 위해 반복해서 파라미터를 조정해 가는것
- 학습률이 너무 작으면 알고리즘이 수렴하기 위해 반복 횟수가 증가하므로 시간이 오래걸린다.
반대로 학습률이 너무 크면, 이전보다 더 높은 곳으로 올라가 적절한 해법을 찾을수 없을 수 있다. - 경사 하강법을 사용할때는 반드시 모든 특성이 같은 스케일을 갖도록 만들어야한다.(StandardScaler() 를 사용)

▷배치 경사 하강법(Batch Gradient Descent)
- 매 경사 하강법 스텝에서 전체 훈련 데이터를 사용
- 매우 큰 훈련 세트에서는 매우 느리다
- 특성수에 민감하지 않음
배치 경사 하강법 비용함수의 편도 함수

경사 하강법의 스텝
→𝜽(next) = 𝜽(now) - *(eta * gradients)
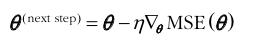
eta = 0.1
n_iterations = 1000
m = 100
theta = np.random.randn(2,1)
for iteration in range(n_iterations) :
gradients = 2/m * (X_b.T.dot(theta) - y) # MSE 비용함수
theta = theta - eta * gradients # 위의 theta 값 갱신
학습률에 따른 그래프 비교

▷확률적 경사 하강법(Stochastic Gradient Descent)
- 매 스탭에서 한 개의 샘플을 무작위로 선택하고 그 하나의 샘플에 대한 그레디언트를 계산
- 매 반복에서 다뤄야 할 데이터의 수가 적기 때문에 빠르다
- 확률적으로 실시하기 때문에, 알고리즘이 배치 경사하강법에 비해 불안정하다

▷미니배치 경사 하강법(MiniBatch Gradient Descent)
- 미니배치를 크게하면 파라미터 공간에서 SGD보다 덜 불규칙적으로 이동

다항회귀
- 주어진 데이터가 단순한 직선의 형태보다 복잡한 형태일때 사용
- 각 특성의 거듭제곱을 새로운 특성으로 추가 후, 확장된 특성을 포함한 데이터셋에 선형 모델을 훈련시킨다
- sklearn.preprocessing에 PolynomialFeatures를 이용(degree를통해 차수를 정할 수 있다)
X_new = np.linspace(-3,3,100).reshape(100,1)
X_new_poly = poly_features.transform(X_new)
y-new = lin_reg.predict(X_new_poly)
plt.plot(X,y,"b.") # 데이터를 파란점으로 표시
plt.plot(X_new,y_new,"r-",linewidth =2 ,label = "Predictions")
plt.xlabel("$x_1$",fontsize = 18)
plt.ylabel("$y$",rotation = 0, fontsize = 18)
plt.legend(loc = "upper left",fontsize = 14)
plt.axis([-3,3,0,10]) # x,y축 범위 설정
plt.show()
차수를 높히면 훈련 데이터 세트에 대해서는 좋은 결과를 받지만, 앞으로 들어오는 데이터에 대해서는 정확성이 떨어질 수 있다. 단순히 차수를 높히는것이 좋은것이 아님
- degree =1 일때는 과소적합, degree = 300일때는 과대 적합이다.
- 적절한 차수를 찾는것이 중요

규제가 있는 선형 모델
▷릿지 회귀
- Linear Regression 에서 l2 규제를 추가한 모델
- 비용함수에 규제항을 추가하면서 학습 알고리즘을 데이터에 맞추는 것 뿐만아니라 모델의 가중치가 가능한 한 작게 유지
- 규제항은 훈련받는 동안에만 비용함수에 추가

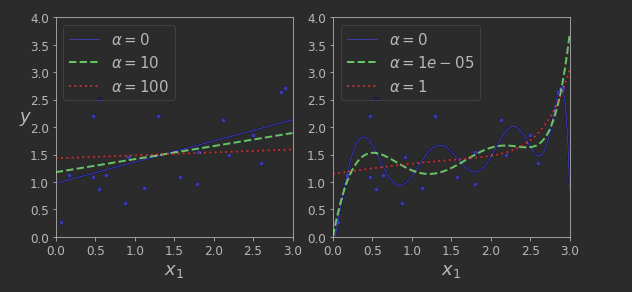
알파(a)값이 0이면 릿지 회귀는 선형회귀와 같아지고 , 아주 크면 모든 가중치가 거의 0에 가까워지기 때문에 결국 데이터의 평균을 지나는 수평선을 지난다
→릿지회귀 정규방정식

→Alpha 값에 따른 Ridge Model 학습
더보기
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=1, solver="cholesky", random_state=42)
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
def plot_model(model_class, polynomial, alphas, **model_kargs):
for alpha, style in zip(alphas, ("b-", "g--", "r:")):
model = model_class(alpha, **model_kargs) if alpha > 0 else LinearRegression()
if polynomial:
model = Pipeline([
("poly_features", PolynomialFeatures(degree=10, include_bias=False)),
("std_scaler", StandardScaler()),
("regul_reg", model),
])
model.fit(X, y)
y_new_regul = model.predict(X_new)
lw = 2 if alpha > 0 else 1
plt.plot(X_new, y_new_regul, style, linewidth=lw, label=r"$\alpha = {}$".format(alpha))
plt.plot(X, y, "b.", linewidth=3)
plt.legend(loc="upper left", fontsize=15)
plt.xlabel("$x_1$", fontsize=18)
plt.axis([0, 3, 0, 4])
plt.figure(figsize=(8,4))
plt.subplot(121)
plot_model(Ridge, polynomial=False, alphas=(0, 10, 100), random_state=42)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(122)
plot_model(Ridge, polynomial=True, alphas=(0, 10**-5, 1), random_state=42)
save_fig("ridge_regression_plot")
plt.show()
▷라쏘 회귀
- 릿지 회귀처럼 선형회귀에 또 다른 규제된 버전
- 비용함수에 규제항을 릿지(1/2 * II l2 ll^2) 대신 가중치 벡터 l1 노름을 사용
- 라쏘 회귀의 중요한 특징은 덜 중요한 특성의 가중치를 제거 -> 자동으로 특성을 선택하고 희소 모델을 만든다
- SGDRegressor(penalty = "l1")으로 사용가능
라쏘회귀의 비용 함수

→Alpha 값에 따른 Lasso Model 학습
더보기
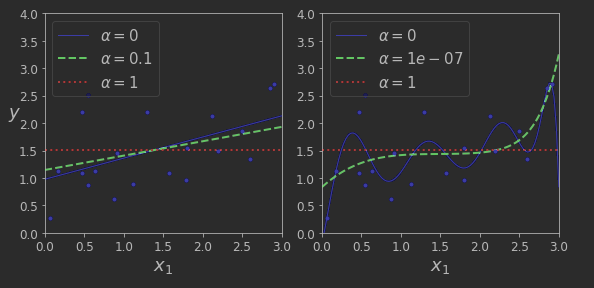
from sklearn.linear_model import Lasso
plt.figure(figsize=(8,4))
plt.subplot(121)
plot_model(Lasso, polynomial=False, alphas=(0, 0.1, 1), random_state=42)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(122)
plot_model(Lasso, polynomial=True, alphas=(0, 10**-7, 1), random_state=42)
save_fig("lasso_regression_plot")
plt.show()
▷ 엘라스틱넷
- 릿지 회귀와 라쏘 회귀를 절충한 모델
- 규제항은 릿지와 라쏘의 규제항을 단순히 더해서 사용하며 혼합정도는 혼합 비율 r을 사용해 조절
- r = 0 일때, 릿디회귀, r= 1 라쏘회귀

Ridge, Lasso, ElasticNet 사용
1.적어도 규제가 약간 있는것이 대부분이므로 일반적으로는 평범한 선형 회귀는 피한다
2.릿지가 기본이 되지만 쓰이는 특성이 적다고 의심되면 라쏘나 엘라스틱 넷을 사용
----> 불필요한 특성의 가중치를 0으로 만듦
3. 특성 수가 훈련 샘플 수 보다 많거나 특성 몇 개가 강하게 연관되어 있을때는 보통 라쏘가 문제를 일으키므로 라쏘보다는 엘라스틱 넷 을 선호
'# AI 이론 > Machine Learning' 카테고리의 다른 글
| K-Means Clustering(K 평균 군집화) 정리 (0) | 2022.04.07 |
|---|---|
| 주성분 분석(PCA)란? (0) | 2022.04.06 |
| [ML]캐글 신용카드 사기 검출 (0) | 2022.02.05 |
| LightGBM (0) | 2022.01.26 |
| XGBoost 소개(파이썬 Wrapper, 싸이킷런 Wrapper) 및 예제 (0) | 2022.01.26 |